FreeR - Hybrid Free Monads for Reduced Quadratic Complexity/Observability & Map-Fusion Optimization in Scala

Draft FreeR code is on Github

Introduction

I’ve recently pushed some Free code & doc to the cool project cats and I had a few more ideas in my head on optimizing Free and never took time to make them concrete. I’ve just found this time during my holidays…

Free Monad is often used to represent embedded DSL in functional programming languages like Haskell or Scala. One generally represents his grammar with a simple Functor ADT representing the available operations. Then, from within your programming language, Free Monad provides the facilities to:

build in a monadic & stack-safe way a static program composed of a sequence of operations,
compile this program,
run it.

To know more about the way to use Free and some more specific theory, please refer to recent draft doc I’ve pushed on cats

The well-known classic representation in Scala is the following:

sealed abstract class Free[F[_], A]
case class Pure[F[_], A](a: A) extends Free[F, A]
case class Suspend[F[_], A](a: F[Free[F, A]]) extends Free[F, A]

Please note that F[_] should be a Functor to take advantage of Free construction.

Building a program can then just be a classic sequence of monadic bind/flatMap on Free[S[_], _]:

for {
  a <- doA(...)
  b <- doB(a, ...)
  c <- doC(c, ...)
} yield (c)

This actually constructs a recursive structure looking like:

Suspend(F(Suspend(F(Suspend(F(....(Pure(a))))))))

It can be seen as a left-associated sequence of operations and as any left-associated structure, appending an element to it has a quadratic complexity. So the more you flatMap, the longer (in n²) it will take to drill down the structure.

So if you try such code:

def gen[I](i: I): Trampoline[I] = Trampoline.suspend(Trampoline.done(i))

//(a flatMap (b flatMap (c flatMap (...))))
def lftBind[S[_]](n: Int)(gen: Int => S[Int])(implicit M: Monad[S]) = {
  (1 to n).foldLeft(gen(0)){ case (acc, i) => acc flatMap { a => gen(i) } }
}

You will see that it has a quadratic curve in terms of execution time when you increase n.

First weakness of classic Free is its left-associativity that induces a quadratic complexity when flatMapping

Solving left-associated quadratic complexity

To solve it, the immediate idea is to make Free right-associative instead of left associative (This idea was proposed by Kiselyov & al. in a paper and called Continuation-Passing-Style or also Codensity construction)

This is already done in current scalaz/cats.Free by adding a new element to the Free ADT:

/** Call a subroutine and continue with the given function. */
sealed abstract class Gosub[S[_], B] extends Free[S, B] {
  type C
  val a: () => Free[S, C]
  val f: C => Free[S, B]
}

If you test the same previous code, it has a linear behavior when n increases.

Quadratic observability

In this great paper Reflection Without Remorse, Atze van der Ploeg & Oleg Kiselyov show that classic Free are subject to another tricky quadratic behavior when, within your sequence of operations, one need to observe the current internal state of Free.

Observing the state requires to drill down the recursive Free structure explicitly and go up and again down then up and again and again. As explained in the paper, this case is quite tricky because it’s very hard to see that it will happen. The deeper is the structure, the longer it takes to observe current state. It’s important to note that right-association doesn’t help in this case and that complexity is once again in O(n²).

The second weakness of Free is its quadratic complexity when observing internal state.

To solve it, in Reflection Without Remorse, they propose a very interesting approach by changing the representation of Free and take advantage of its sequential nature.

A Free becomes the association of 2 elements:

a FreeView representing current internal state of the Free
a sequence of bind/flatMap functions stored in an efficient data structure that can prepent/append in O(1).

For the data structure, they propose to use a type-aligned dequeue to keep track of all types.

I have tried to implement this structure using a typed-aligned FingerTree in Scala. The code is here. The result is pretty interesting but not much efficient: it has a linear behavior for left-association & observability but…

for lower values of n, FingerTree costs far too much to build
memory cost is so high that it triggers the JVM GC far too soon and limitates a lot what you can do
allocated memory locality isn’t good and requires huge amounts of memory jumps.
type-alignment makes code quite ugly (yes Scala type inference isn’t as powerful as Haskell in this case and laziness of Haskell helps a lot for FingerTree)

As a conclusion, the idea is really nice on paper but in practice, we need to find something that costs less than this type-aligned dequeue (even if my FingerTree code is really raw, too strict and not optimized at all).

FreeR hybrid structure

I wanted to improve Free behavior and decided to create a new version of it called FreeR thinking in terms of efficient Scala…

I really liked the idea of representing a Free as a pure sequence of operations with a view of current internal state.

To gain in efficiency, I decided to choose another efficient append/prepend data structure, optimized and very well known: Vector providing:

append/prepend in O(1) (in average),
random access in constant time,
quite good locality.

Then, I’ve decided to relax a lot type alignment and manipulate Any values internally and cast/reify to the right types when required.

BTW, I plagiarized some code written by Alois Cochard for his new IO model in Scalaz/8.0 branch… Alois is a great dev & had made concrete the idea I had in my head so why rewrite them differently? uh ;)

I also decided to reify the 2 kinds of operations:

Bind for flatMap/bind calls
Map for map calls

So a Free becomes:

// to mitigate the shock of Any in the code
// and provide helpers for casting/reifying
type Val = Any

case class FreeR[S[_], A](
  head: FreeView[S, Val],
  ops: Ops = Vector.empty
) extends FreeR[S, A]

with FreeView as:

// The view of Free internal state can be of 2 types:
sealed abstract class FreeView[S[_], A]

object FreeView {
  // Pure value
  case class Pure[S[_], A](a: A) extends FreeView[S, A]

  // Impure computation determined by the Functor S
  case class Impure[S[_], A](a: S[FreeR[S, A]]) extends FreeView[S, A]
}

and Ops are:

sealed trait Op
object Op {
  case class Map(f: Val => Val) extends Op
  case class Bind[S[_]](f: Val => FreeR[S, Val]) extends Op
}

FYI This code is less than 300 lines so nothing really horrible except a few ugly casts ;)

Left Association

The code used for testing can be found here

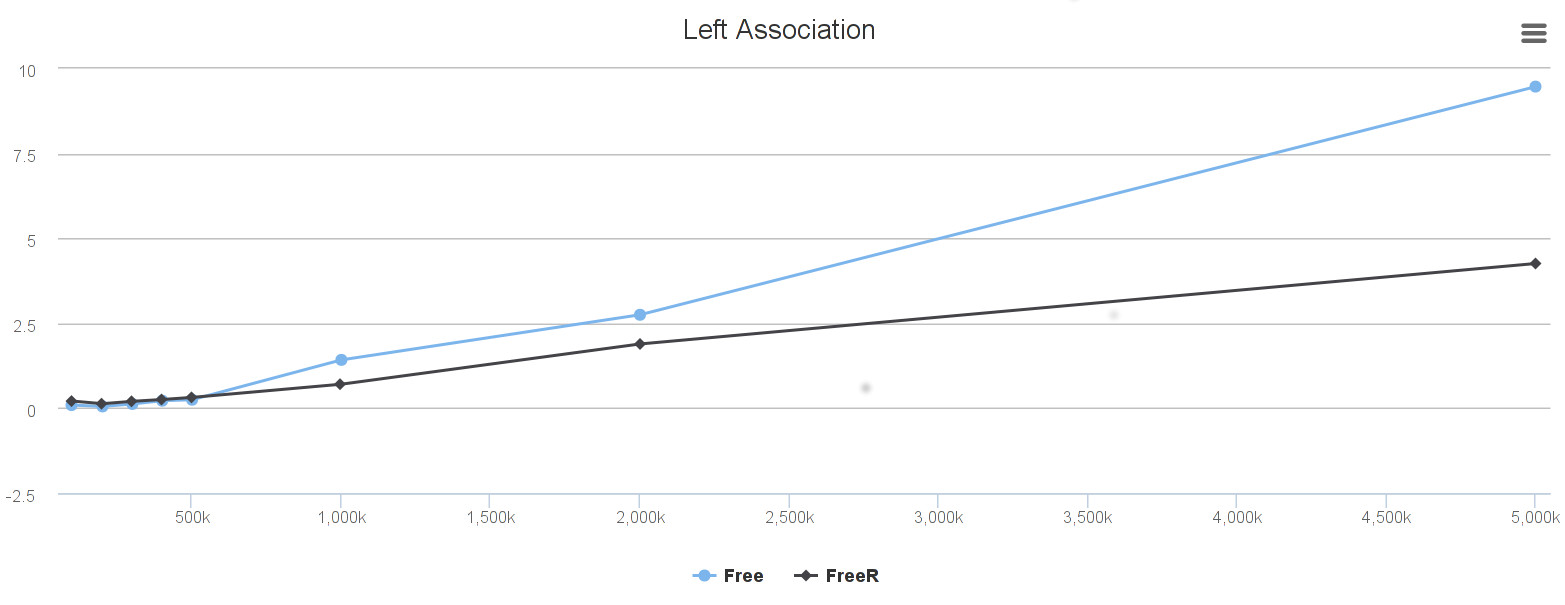
FreeR behavior is linear even for millions of flatMap (until the GC triggers naturally) whereas classic Free has clearly quadratic curve.

Observability

The code used for testing can be found here

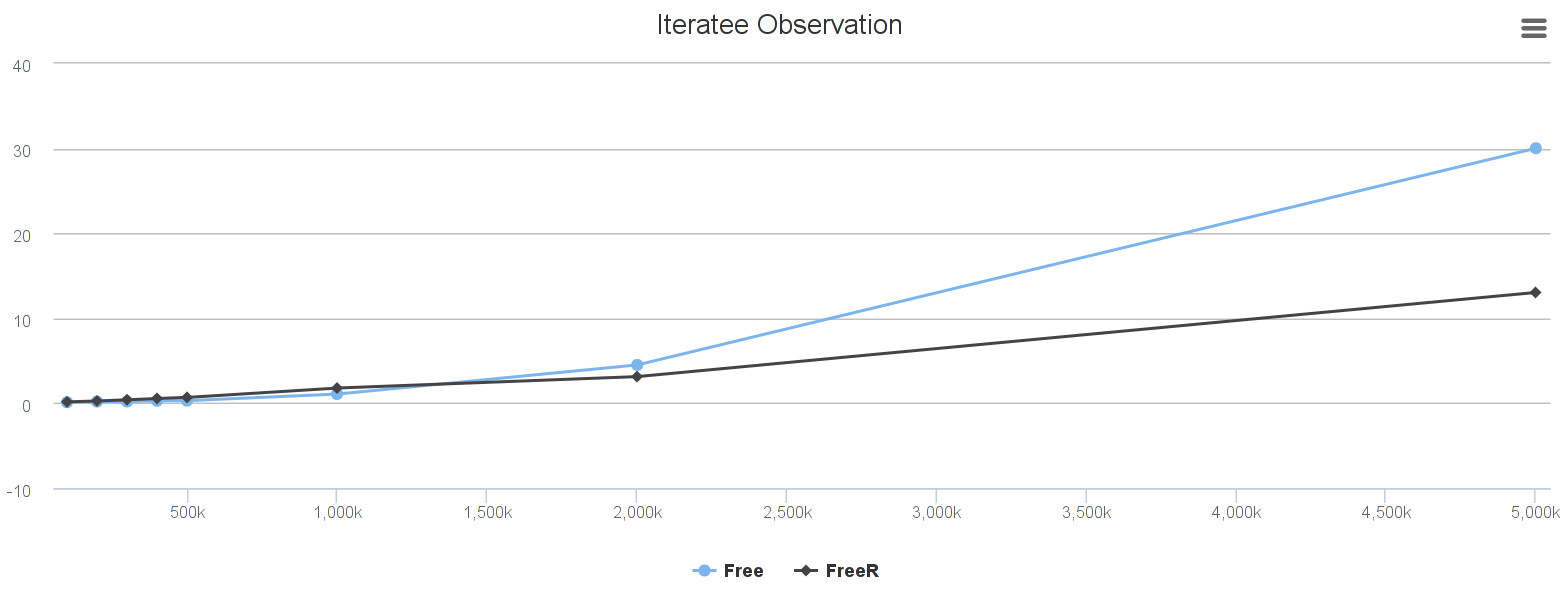
FreeR behavior is quite linear even for millions of flatMap (until the GC triggers naturally) whereas classic Free has clearly quadratic curve.

Right association complexity

I finally tried to check the behavior of my new FreeR when using flatMap in a right associated way like:

// (... flatMap (_ => c flatMap (_ => b flatMap (_ => a))))
def rgtBind[S[_]](n: Int)(gen: Int => S[Int])(implicit M: Monad[S]) = {
  (1 to n).foldLeft(gen(n)){ case (acc, i) => gen(n-i) flatMap { _ => acc } }
}

This is not so frequent code but anyway, Free should be efficient for left & right associated code.

Using FreeR as described previously, I’ve discovered that it wasn’t efficient in right association when increasing n because it allocates recursively a lot of Vector with one element and it becomes slower and slower apparently (I’m not even sure of the real cause of it).

I’ve refined my representation by distinguishing 3 kinds of Free in my ADT:

// No op
case class FreeR0[S[_], A](head: FreeView[S, Val]) extends FreeR[S, A]

// One single op (typically the right association case)
case class FreeR1[S[_], A](head: FreeView[S, Val], op: Op) extends FreeR[S, A]

// Multiple ops
case class FreeRs[S[_], A](head: FreeView[S, Val], ops: Ops = Vector.empty) extends FreeR[S, A]

With this optimization, here is the performance in right association:

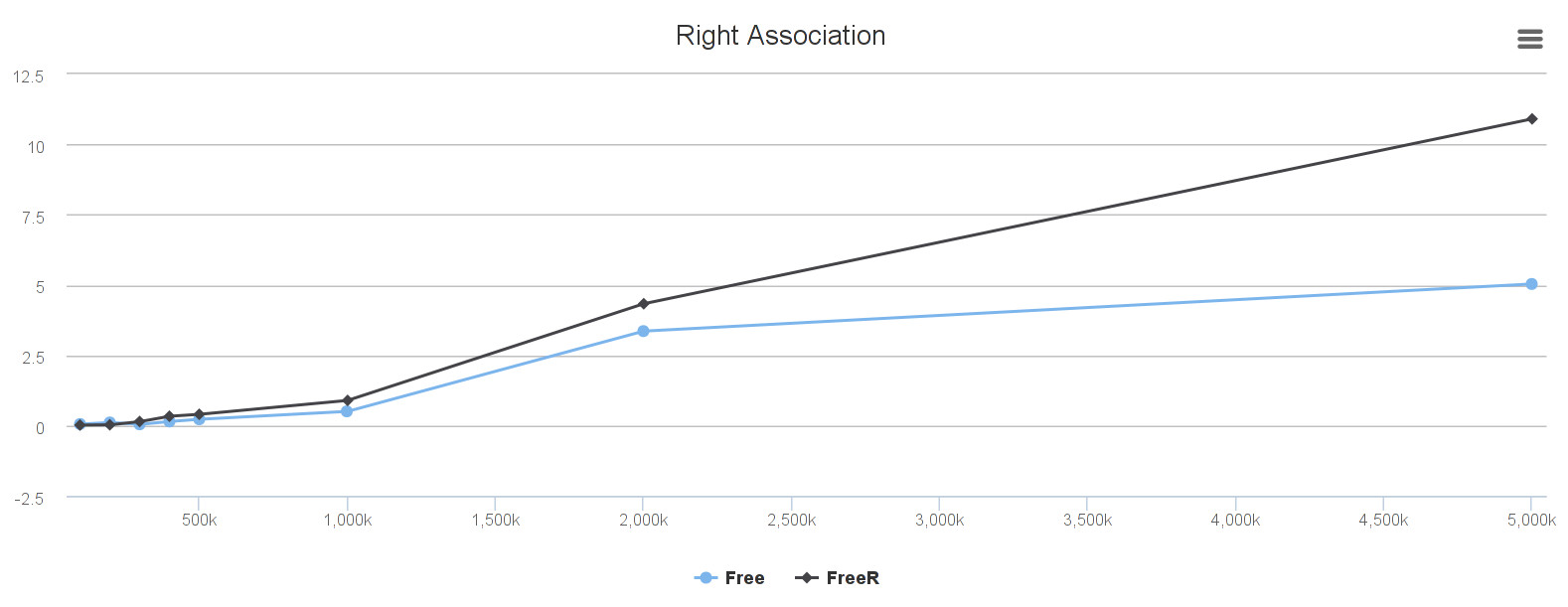
It is quite comparable to classic Free for n under 1 million but it becomes quite bad when n becomes big. Yet, it remains for more efficient than previous representation with just Vector.

I need to work more on this issue (apparently GC is triggered too early) to see if more optimizations for right association can be found…

Cherry on the cake: map-fusion optimization

Imagine doing a lot of map operations on a Free like:

def mapalot(n: Int): Trampoline[Long] = {
  (1 to n).foldLeft(Trampoline.done(0L)){ case (acc, i) => acc map { a => a + 1 } }
}

If you think just a bit, you will clearly see that:

a.map(f).map(g) == a.map(g compose f)

This is called map-fusion and as you may have deduced already, my decision to reify explicitly Bind and Map operations was made in this purpose.

If I can know there are several Map operations in a row, I can fusion them in one single Map by just calling mapFusion on a Free to optimize it:

val free = FreeRTools.mapalot(x)

// optimized free
val freeOpt = free.mapFusion

// run the trampoline
freeOpt.run

Here is the difference in performance between FreeR and FreeR.mapFusion:

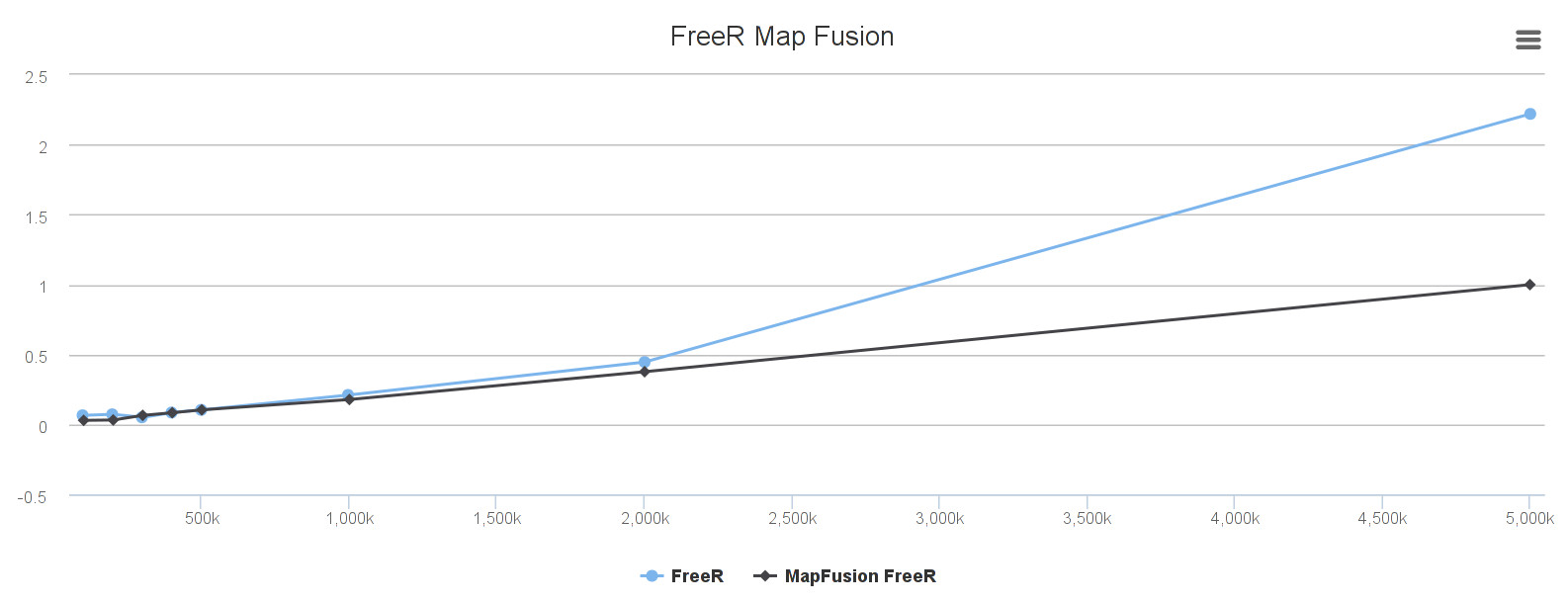
As you can see, mapFusion can be very interesting in some cases.

Conclusion

Finally, I have created a new representation of Free using:

type-relaxed version of Reflection w/o Remorse
sequence of operations managed by Scala Vector
reification of Bind & Map operations
differenciation of None/Single/Multiple operations cases
Map Fusion optimization

It allows to have a Free with:

Linear behavior in Left-Assocation, Observability,
Stack-safety is sill ensured,
Right-Association should be optimized because it still has a too high cost for bigger n (yet it is far more acceptable than other alternatives),
Map Fusion can provide an interesting optimization when using multiple consecutive Map operations,
For small n, the cost is a bit higher than basic Free but quite low and acceptable.

It is really interesting as it makes Free more and more usable in real-life problems without having to rewrite the code bootstrapped with Free in a more optimized way. I personally find it quite promising!

Please remark that this code has been written for the great project cats that will soon be a viable & efficient alternative for functional structures in Scala.

The full code is there.

Don’t hesitate to test, find bugs, contribute, give remarks, ideas…

Have fun in FreeR world…